Árboles de regresión y random forest para regresión y clasificación
Publicado: <2022-03-18 Fri>

La matriz de correlación indicará que tan fuerte o débil es la relación entre dos variables. Puede leerse por columnas o por filas. En la siguiente imagen se eliminó la columna Id, porque no será relevante para el análisis. La claridad de la celda es directamente proporcional a una mayor correlación.

df_train = df_train.drop(columns = ['Id'])
plt.figure(figsize=(20,8),dpi=80)
corrmat = df_train.corr()
sns.heatmap(corrmat, vmax=.8, fmt='.1f', annot=True)

<AxesSubplot:>

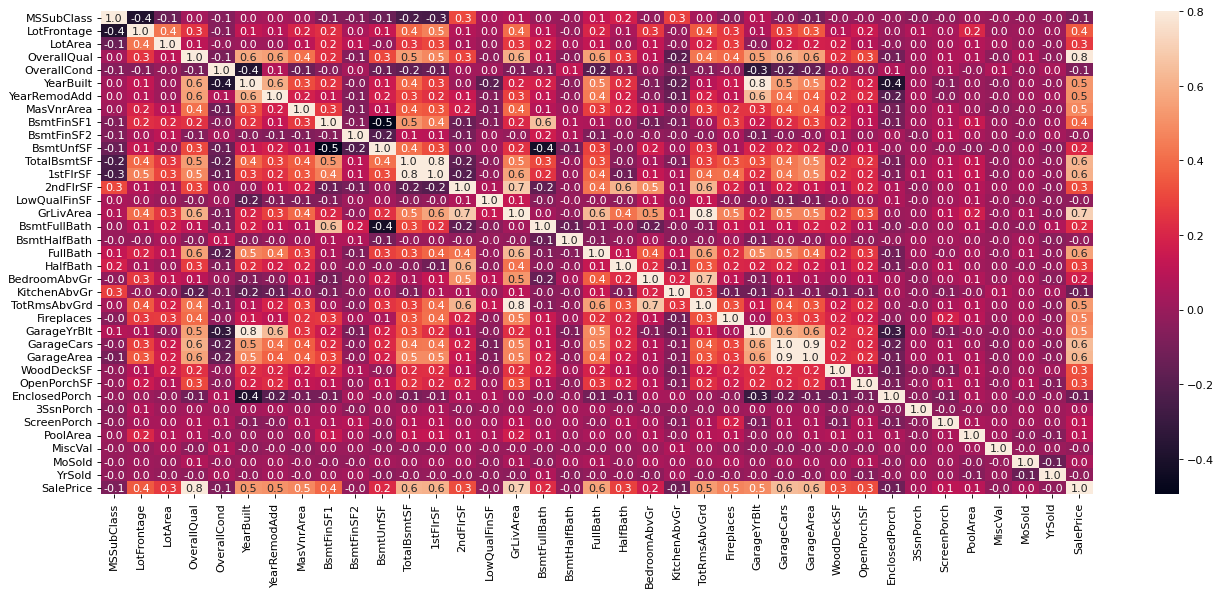
De esta forma podemos saber que variables están más relacionadas con otras. en el caso de la variable SalePrice las diez variables más útiles serán aquellas con mayor índice de correlación, mismas que se usarán posteriormente para las predicciones.

df_train.corr()['SalePrice'].sort_values(ascending=False)[1:11]

OverallQual     0.790982
GrLivArea       0.708624
GarageCars      0.640409
GarageArea      0.623431
TotalBsmtSF     0.613581
1stFlrSF        0.605852
FullBath        0.560664
TotRmsAbvGrd    0.533723
YearBuilt       0.522897
YearRemodAdd    0.507101
Name: SalePrice, dtype: float64

Para ubicar si una celda tiene un valor vacío se usa la función isnull(), si se prefiere lógica inversa se usa notnull. Es posible obtener un vector de estos valores con la propiedad values, transformarlo a un array con la función ravel() y sumar los valores verdaderos con la función sum(). También es posible obtener una lista ordenada de las columnas con más valores vacíos.

df_train.isnull().sum().sort_values(ascending=False)[0:19]

PoolQC          1453
MiscFeature     1406
Alley           1369
Fence           1179
FireplaceQu      690
LotFrontage      259
GarageYrBlt       81
GarageCond        81
GarageType        81
GarageFinish      81
GarageQual        81
BsmtExposure      38
BsmtFinType2      38
BsmtCond          37
BsmtQual          37
BsmtFinType1      37
MasVnrArea         8
MasVnrType         8
Electrical         1
dtype: int64

En el ejemplo de arriba, el valor es el número de valores vacíos, si usamos la función notnull() sería el número de valores no vacíos, la suma de ambos debe ser el número total de filas obtenido anteriormente.

Hay dos razones para la falta de valores en los datasets:

• Recolección de datos: No se consiguieron los datos.
• Extracción de datos: Los datos están en la DB original pero no se extrajeron correctamente al dataset.

Se deben evitar datos vacíos para no tener problemas de manejo de información. Se tienen dos opciones:

• Borrar las filas donde falten valores en alguna de las columnas
• Borrar las columnas donde no se tenga suficiente información

En este ejercicio es posible observar que las columnas MiscFeature, Fence, PoolQC, FirePlaceQu y Alley tienen muy pocos valores proporcionados (menos del 55 por ciento)y no vale la pena conservarlas. Otro criterio para asegurar un buen curso de acción es revisar las correlaciones con la columna SalePrice.

Como el razonamiento es el correcto se procede al borrado de columnas.

def toDel(df):
    for col in df.columns.values:
        nv = pd.isnull(df[col]).values.ravel().sum()
        if nv > df.shape[0] * 0.45:
            print("Deleting: "+col)
            del df[col]
    return df
df_train = toDel(df_train)

Deleting: Alley
Deleting: FireplaceQu
Deleting: PoolQC
Deleting: Fence
Deleting: MiscFeature

Es necesario detectar nuevamente que columnas tienen valores vacíos. Esta vez se reemplazarán esos valores. Hay valores númericos y categóricos vacíos; los numéricos serán reemplazados por el promedio original de la columna, los categóricos serán remplazados por el valor no nulo más cercano puede ser el valor que va antes (ffill) o el que va después (bfill), en este análisis será el segundo.

Es necesario señalar que el procedimiento más preciso para las columnas categóricas sería colocar el valor de mayor frecuencia relacionado con el valor de la columna objetivo, por ejemplo: Si la columna Y del dataframe es la variable dependiente y X es una columna categórica con valores perdidos; dichos valores se llenarán por aquel de mayor frecuencia en X tomando en cuenta solo aquellos con los que coincidan en Y. Más adelante se retomará la justificación de porque no se ha hecho de esta forma.

def DetectNull(df):
    candidates = []
    for col in df.columns.values:
        nv = pd.isnull(df[col]).values.ravel().sum()
        if nv > 0:
            candidates.append((col, df[col].dtype, nv))
    return candidates

def FillNull(df, list):
    for col in list:
        if col[1] == 'float64':
            df[col[0]] = df[col[0]].fillna(df[col[0]].mean())
        else:
            df[col[0]] = df[col[0]].fillna(method="bfill")
    return df

df_test = FillNull(df_test, DetectNull(df_test))
df_train = FillNull(df_train, DetectNull(df_train))
df_train.isnull().sum().sort_values(ascending=False)

MSSubClass      0
GarageYrBlt     0
Fireplaces      0
Functional      0
TotRmsAbvGrd    0
               ..
MasVnrArea      0
MasVnrType      0
Exterior2nd     0
Exterior1st     0
SalePrice       0
Length: 75, dtype: int64

Primero serán creados los conjuntos de prueba y entrenamiento. Serán usados para el modelo solo aquellos campos que tengan un alto índice de correlación en la matriz de correlaciones mostrada anteriormente.

train, test = train_test_split(df_train, test_size=0.2)
predictors = ['OverallQual', 'GrLivArea', 'GarageCars', 'GarageArea', 'TotalBsmtSF', '1stFlrSF', 'FullBath', 'TotRmsAbvGrd', 'YearBuilt', 'YearRemodAdd']
target = ['SalePrice']

A continuación se entrena el árbol de regresión y se ingresan los datos para probar la predicción del mismo.

dtr = DecisionTreeRegressor(max_depth=15, min_samples_split=20, random_state=99)
dtr.fit(train[predictors], train[target])
prediction = dtr.predict(test[predictors])

Ahora se muestran los resultados: una comparación entre los datos originales y las predicciones, además, el árbol obtenido, mismo que fue guardado en la carpeta out del proyecto en formato graphviz y como imagen.~\citep{Galarnyk_2021}

test['preds'] = prediction
test[['SalePrice','preds']]

      SalePrice          preds
520      106250   62509.090909
562      108000  130822.222222
265      175500  176128.571429
1228     367294  337085.071429
280      228500  199144.444444
...         ...            ...
670      173500  176352.631579
102      118964  136842.947368
1130     135000  145525.777778
1016     203000  263613.333333
12       144000  119778.571429

[292 rows x 2 columns]

En la tabla se observa que muchos valores de predicción están repetidos, esto se debe a que entran en la misma lógica de predicción. Debe recordarse que el árbol funciona decidiendo con valores preestablecidos.

with open('out/dtr.dot','w') as dotfile:
    export_graphviz(dtr, out_file=dotfile, feature_names=predictors)
    dotfile.close()

tree.plot_tree(dtr);

Para validar el modelo se usará un método de validación cruzada, un método estadístico para evaluar y comparar algoritmos de aprendizaje dividiendo datos en dos segmentos: entrenamiento y prueba. Típicamente, ambos conjuntos deben cruzarse en rondas sucesivas de modo que cada punto de datos tenga la posibilidad de ser validado. La forma básica es la validación cruzada k-fold.~\citep{Refaeilzadeh_Tang_Liu_2018}

dtr = DecisionTreeRegressor(max_depth=15, min_samples_split=20, random_state=99)
dtr.fit(train[predictors], train[target])
cv = KFold(n_splits = 20, shuffle = True, random_state = 1)
score = np.mean(cross_val_score(dtr, train[predictors], train[target], scoring = "neg_mean_squared_error", cv = cv, n_jobs = 1))
score

-1695546565.4410434

El modelo es muy deficiente según el error cuadrático medio de pérdida. Este error es muy grande, debería ser cercano a cero. Sería mejor probar un modelo lineal, los árboles de regresión son útiles si es necesario estimar un modelo no lineal. Para confirmar se realizará este modelo bajo diferentes profundidades del árbol, de esta forma se podría encontrar un mejor conjunto de parámetros, no sucede en este caso.

for i in range(1,21):
    dtr = DecisionTreeRegressor(max_depth=i, min_samples_split=20, min_samples_leaf=5,random_state=99)
    dtr.fit(train[predictors], train[target])
    cv = KFold(n_splits = 20, shuffle = True, random_state = 1)
    score = np.mean(cross_val_score(dtr, train[predictors], train[target], scoring = "neg_mean_squared_error", cv = cv, n_jobs = 1))
    print("Score para i=",i,": ",score)

Score para i= 1 :  -3518061167.0543084
Score para i= 2 :  -2579254167.548243
Score para i= 3 :  -2153519070.3027043
Score para i= 4 :  -1785517029.0882308
Score para i= 5 :  -1658794897.3649328
Score para i= 6 :  -1611813883.5452306
Score para i= 7 :  -1551394173.9604716
Score para i= 8 :  -1554754004.1369624
Score para i= 9 :  -1547076489.8592367
Score para i= 10 :  -1551932650.1670842
Score para i= 11 :  -1551095985.7058103
Score para i= 12 :  -1551446872.7832217
Score para i= 13 :  -1551400950.2026584
Score para i= 14 :  -1549894543.9422781
Score para i= 15 :  -1550710493.3735516
Score para i= 16 :  -1552723780.9771752
Score para i= 17 :  -1552723780.9771752
Score para i= 18 :  -1552723780.9771752
Score para i= 19 :  -1552723780.9771752
Score para i= 20 :  -1552723780.9771752

Al igual que en la sección anterior, se entrena el modelo con los mismos conjuntos definidos anteriormente y se hace una predicción.

rfr = RandomForestRegressor(n_jobs = 1, oob_score=True, n_estimators=10000)
rfr.fit(train[predictors], train[target].values.ravel())
prediction = rfr.predict(test[predictors])
test['preds'] = prediction
test[['SalePrice','preds']]

      SalePrice          preds
520      106250   96389.837800
562      108000  107334.079900
265      175500  178429.007700
1228     367294  332232.461100
280      228500  211677.532000
...         ...            ...
670      173500  176562.496908
102      118964  129663.313500
1130     135000  140604.314200
1016     203000  230900.547700
12       144000  113294.444000

[292 rows x 2 columns]

Como puede verse, un bosque de diez mil árboles las estimaciones los valores se acercan notablemente. Esto puede confirmarse con la puntuación propia del bosque, la cual funciona como el coeficiente de determinación de un modelo de regresión.

rfr.oob_score_

0.8086789376427154

La conclusión es que sería mejor usar un modelo de regresión que un modelo de decisión porque pese a la mejora sustancial respecto al árbol anterior, el bosque no alcanza un 0.9 en la puntuación, condición que se le exigiría a un modelo lineal. Debido a que este es el mejor modelo obtenido, lo usaremos para df_test.

df_test['SalePrice'] = rfr.predict(df_test[predictors])
df_test.to_csv('out/housing_test_complete.csv')

Ahora se procederá a crear categorías con la columna SalePrice. Para ello se ha escrito una función y una nueva columna dentro del dataframe.

def SalePriceGroupValue(x):
    if x >= 500001:
        return 'G3'
    elif x <= 100000:
        return 'G1'
    return 'G2'
df_train["SalePriceGroup"] = df_train["SalePrice"].apply(SalePriceGroupValue)
df_train["SalePriceGroup"].value_counts()

G2    1328
G1     123
G3       9
Name: SalePriceGroup, dtype: int64

Aquí es posible observar que la gran mayoria de los datos se encuentran en la categoría G2. Esto confirma que la opción antes seleccionada para llenar datos perdidos es buena debido a que binda una posibilidad de preservar datos las otras categorías.

Se repetirá el procedimiento visto anteriormente, la diferencia es que ahora usará DecisionTreeClassifier.~\citep{Navlani_2018}

train, test = train_test_split(df_train, test_size=0.2)

colnames = df_train.columns.values.tolist()
predictors = ['OverallQual', 'GrLivArea', 'GarageCars', 'GarageArea', 'TotalBsmtSF', '1stFlrSF', 'FullBath', 'TotRmsAbvGrd', 'YearBuilt', 'YearRemodAdd']
target = colnames[75]
dtc = DecisionTreeClassifier(criterion="entropy", max_depth=3, min_samples_split=20, random_state=99)
dtc.fit(train[predictors], train[target])
prediction = dtc.predict(test[predictors])

Se ha creado una tabla cruzada que logra visualizar los resultados, además es posible usar metricas simples para verificar la exactitud del árbol.

pd.crosstab(test[target], prediction, colnames=["Predictions"], rownames=["Real"])

Predictions  G1   G2
Real                
G1           10   11
G2           12  257
G3            0    2

print("Accuracy: ", metrics.accuracy_score(prediction, test[target]))

Accuracy:  0.9143835616438356

with open('out/dtc.dot','w') as dotfile:
    export_graphviz(dtc, out_file=dotfile, feature_names=predictors)
    dotfile.close()

tree.plot_tree(dtc);

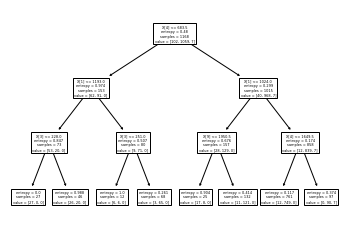
Al usar nuevamente validación cruzada se observa que una buena clasificación esta entre i=3 e i=6, lo que significa que si se deja crecer el árbol desde el nodo raíz con estas profundidades es posible obtener clasificaciones óptimas. También podemos ver que las variables de mayor importancia clasificatoria son TotalBsmtSF y GrLivArea.

for i in range(1,10):
    dtc = DecisionTreeClassifier(criterion="entropy", max_depth=i, min_samples_split=20, random_state=99)
    dtc.fit(train[predictors], train[target])
    cv = KFold(n_splits = 20, shuffle = True, random_state = 1)
    score = np.mean(cross_val_score(dtc, train[predictors], train[target], scoring = "accuracy", cv = cv, n_jobs = 1))
    print("Score para i=",i,": ",score)
    print("Importancia de variables: \n\t",dtc.feature_importances_)

Score para i= 1 :  0.9066481589713618
Importancia de variables: 
       [0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]
Score para i= 2 :  0.9323641145528929
Importancia de variables: 
       [0.         0.46494326 0.         0.         0.53505674 0.
 0.         0.         0.         0.        ]
Score para i= 3 :  0.9332261835184102
Importancia de variables: 
       [0.         0.33238498 0.         0.09651566 0.46853394 0.
 0.         0.         0.         0.10256542]
Score para i= 4 :  0.9366306253652835
Importancia de variables: 
       [0.         0.31621815 0.         0.07775052 0.41561868 0.02302104
 0.         0.         0.06193988 0.10545173]
Score para i= 5 :  0.9391729982466395
Importancia de variables: 
       [0.02617778 0.31151851 0.         0.08319446 0.38373239 0.02125486
 0.         0.         0.03762721 0.13649479]
Score para i= 6 :  0.939187609585038
Importancia de variables: 
       [0.02517877 0.31133357 0.         0.08882965 0.37821928 0.02044373
 0.         0.         0.03619127 0.13980373]
Score para i= 7 :  0.9383255406195208
Importancia de variables: 
       [0.03296921 0.30531763 0.01780554 0.07541623 0.35646125 0.01926765
 0.         0.         0.06100131 0.13176117]
Score para i= 8 :  0.9340590298071303
Importancia de variables: 
       [0.03224009 0.28731886 0.01741177 0.07374839 0.35982465 0.02625347
 0.         0.         0.06609772 0.13710506]
Score para i= 9 :  0.9331969608416131
Importancia de variables: 
       [0.03174187 0.29167446 0.0171427  0.07260873 0.35426417 0.02584777
 0.         0.         0.07173396 0.13498634]

En la implementación de este bosque se usa el mismo procedimiento visto anteriormente, es importante poner atención en los cambios de los argumentos de cada árbol, cada implementación dependerá del problema.

rfc = RandomForestClassifier(n_jobs = 1, oob_score=True, n_estimators=10000)
rfc.fit(train[predictors], train[target])
prediction = rfc.predict(test[predictors])
test['preds'] = prediction
test[['SalePriceGroup','preds']]

     SalePriceGroup preds
1378             G1    G1
218              G2    G2
1328             G2    G2
194              G2    G2
919              G2    G2
...             ...   ...
415              G2    G2
1227             G2    G2
928              G2    G2
1354             G2    G2
362              G2    G2

[292 rows x 2 columns]

En esta ocasión se ha aumentado la exactitud del árbol, es posible decir que se ha creado un modelo confible. Debido a que este es el mejor modelo obtenido, lo usaremos para df_test.

rfc.oob_score_

0.9417808219178082

df_test['SalePriceGroup'] = rfc.predict(df_test[predictors])
df_test.to_csv('out/housing_test_complete.csv')